نظریه گراف (Graph theory) شاخهای از ریاضیات است که درباره گرافها بحث میکند. در این فایل Word که برای دانلود قرار داده شده است به آموزش این مبحث و کاربردهای آن پرداخته میشود.
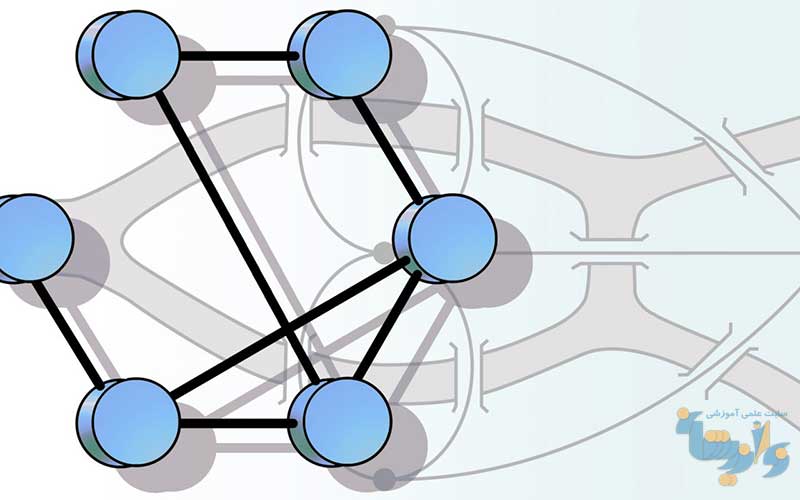
در دنياي اطراف ما، وضعيتهاي فراواني وجود دارند كه ميتوان توسط نموداري متشكل از يك مجموعه نقاط، به علاوه خطوطي كه برخي از اين نقاط را به يكديگر متصل ميكنند، به توصيف آنها پرداخت. به عنوان مثال، براي نشان دادن رابطه دوستي بين يك دسته از انسانها ميتوانيم هر شخص را با يك نقطه مشخص كنيم. نقاط متناظر با هر دو دوست را با يك خط به يكديگر وصل نماييم، يا در جاي ديگر ممكن است براي نشان دادن يك شبكه ارتباطي، از نموداري استفاده كنيم كه در آن، نقاط نمايانگر مراكز ارتباطي و خطوط، نشاندهنده پيوندهاي ارتباطي بين مراكز باشند.
اگر يك گراف، نموداري داشته باشد كه در آن يالها تنها در راسهاي دو سر خود متقاطع باشند، مسطح ناميده ميشود، چون ميتوان به سادگي اين گونه گرافها را روي يك صفحه مسطح رسم كرد. دو راس كه برروي يال مشتركي واقعند، مجاور ناميده ميشوند. به همين ترتيب دو يال واقع بر روي يك راس مشترك نيز مجاورند. يك يال با دو سر يكسان، طوقه و يك يال با دو سر متمايز، يال پيوندي ناميده ميشود. اگر مجموعه راسها و مجموعه يالهاي يك گراف، متناهي باشند، گراف مزبور را متناهي مينامند. گرافي را كه يك راس داشته باشد بديهي و ساير گرافها را غير بديهي ميناميم.
فهرست مطالب نظریه گراف و کاربردهای آن :
فصل اول: مقدمه
- آشنایی با گراف
- يك ريختي گرافها
- ماتريس وقوع – مجاورت
- زير گرافها
- درجه راسها
- مسيرها
- دورها
- مساله كوتاهترين مسير
فصل دوم: درختها
- يالهاي برشي و باندها
- راسهاي برشي
- فرمول كيلي
- مساله ارتباطدهي
فصل سوم: همبندی
- ساخت شبكههاي ارتباطي قابل اعتماد
- تورهاي اويلري و دورهاي هميلتني
- دورهاي هميلتني
- مساله پستچي چيني
- الگوريتم فلوري
- مساله فروشنده دورهگرد
فصل چهارم: تطابقها
- تطابقها و پوششها در گرافهاي دو بخشي
- تطابق كامل
- رنگآميزي يالي
- قضيه ويزينگ
- مساله زمانبندي
 نواندیشان | بهترین سایت علمی آموزشی کشور
نواندیشان | بهترین سایت علمی آموزشی کشور