نواندیشان | بهترین سایت علمی آموزشی کشور
سیاه چاله و نسبیت عام
اينشتين در نوجوانى علاقه چندانى به تحصيل نداشت. پدرش از خواندن گزارش هايى كه آموزگاران درباره پسرش مى فرستادند، رنج مى برد. گزارش ها حاكى از آن بودند كه آلبرت شاگردى كندذهن، غيرمعاشرتى و گوشه گير است. در مدرسه او را ?باباى كند ذهن ? لقب داده بودند. او در ۱۵ سالگى ترك تحصيل كرد، در حالى كه بعدها به خاطر تحقيقاتش جايزه نوبل گرفت .
شايد شما نيز اين جملات را خوانده يا شنيده باشيد و شايد اين پرسش نيز ذهن شما را به خود مشغول كرده باشد كه چگونه ممكن است شاگردى كه از تحصيل و مدرسه فرارى بوده است، برنده جايزه نوبل و به عقيده برخى از دانشمندان، بزرگ ترين دانشمندى شود كه تاكنون چشم به جهان گشوده است؟
ولی چه باید کرد ؟ درست 27 سال همان بابای کند ذهن بزرگترین جایزه ی علمی جهان را در رشته فیزیک برای کارش در زمینه ی اثر فوتوالکتریک دریافت کرد . شاید بتوان گفت که او در سال در 1915 با ارائه ی نسبیت عام بزرگترین انقلاب فکری را در تمام دوران فیزیک برپا کرد . زمانی که در سال 1919 نظریه ی او یعنی نسبیت عام بعینه مشاهده شد او به شهرت جهانی رسید به گفته ی خودش تنها چیزی او را به این سمت کشاند نیروی جالبی بود که بروی عقربه های قطب نمایی که پدرش در کودکی برای او خریده بود تأثیر می گذاشت بعد از این مقدمه ی نسبتا” طولانی بد نیست به نسبیت عام بپردازیم.
نسبیت عام حاصل پنج سال تلاش بی وقفه اینشتین بود . اینشتین در نسبیت عام از هندسه نا اقلیدسی کمک گرفت . اما چگونه ؟ لازم است نیم نگاهی به این هنسه بیندازیم .
همانطور که می دانیم هندسه اقلیدسی هندسه صفحه نیز نامیده می شود . این هندسه دارای پنج اصل است که تمام وضعیات خطوط در صفحه با توجه به آن مشخص می شود . این پنج اصل به شرح زیر هستند .
اصل اول – از هر نقطه مي توان خط مستقيمي به هر نقطه ي ديگر كشيد .
اصل دوم – هر پاره خط مستقيم را مي توان روي همان خط به طور نامحدود امتداد داد
اصل سوم – مي توان دايره اي با هر نقطه دلخواه به عنوان مركز آن و با شعاعي مساوي هر پاره خط رسم كرد
اصل چهارم – همه ي زواياي قائمه با هم مساوي اند
اصل پنجم – از يك نقطه خارج يك خط، يك خط و و تنها يك خط مي توان موازي با خط مفروض رسم كرد
گروهی از ریاضیادان ها بروی اصل موضوعه ی پنجم شک کردند و با کار بروی این اصل توانستند در شرایطی خاص آن را نقض کنند البته گفتنی است که دانشمندانی چون خیام و پدر بویوئی بروی این اصل بسیار کار کردند ولی به نتیجه مطلوب دست نیافتند .
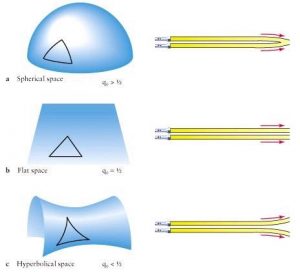
ولی سرانجام یانوش بویوئی و لباچوفسکی برای نخستین بار یکی از انوع این هندسه را کشف کردند . از این نوع هندسه انواع گوناگونی وجود دارد که همه ی آنها در اصل موضوعه ی پنجم با هم اختلاف آشکاری دارند . با توجه به اصل دوم می توانیم دو حالت غیر از این حالت را بیان کنیم حالت اول این است که بگوئیم که ما قادریم بیش از یک خط موازی رسم کنیم این همان کاری است که بویوئی و لباچوفسکی انجام دادند این هندسه ، هندسه هذلولی نیز نامیده می شود که در آن مجموع زوایای درونی یک مثلث کمتر از 180 است و نسبت محیط به قطر بیشتر از عدد پی است . انحنای خط در این حالت منفی است .
گرانش اثر هندسی جرم بر فضا زمان اطراف خود است
هندسه ی هذلولی برای کار در نسبیت عام به کار نیامد پس آلبرت اینشتین از هندسه ی بیضوی که در سال 1854 توسط فردریک ریمان تدوین شده بود استفاده کرد . این هندسه در اصل پنجم دقیقا” خلاف هندسه ی هذلولی است . یعنی این هندسه به وضوح می گوید از یک نقطه خارج یک خط هرگز نمی توان خطی موازی با آن رسم کرد . این هندسه به طور مطلق و کامل به کار نسبیت عام می آمد . البته او تبصره ای در اصل دوم نیز گذاشت و گفت اگر نا متناهی بودن آن را به بی کرانگی بودن تبدیل کنیم در این صورت این هندسه به وجود می آید . زیرا در این هندسه اگر بروی سطح مورد نظر هر چقدر هم که بی کران باشد حرکت کنیم ( بر خط راست ) سرانجام می توانیم به نقطه ی اول بازگردیم . در این هندسه مجموع زوایای درونی مثلث بیشتر از 180 درجه است و انحنا خط مثبت است . همچنین باید بدانیم که نباید برای هر کدام درستی یا نادرستی تعیین کنیم زیرا هر کدام چه هندسه اقلیدسی و چه نا اقلیدسی با توجه به انحنا خط در جایی خاص کاربرد دارند .
میتوانید متن کامل این مقاله تحقیقی را در11 صفحه از لینک زیر دانلود کنید.
